Virtual Passive Control of Linear Dynamic Systems in Second-Order Form

In this work we derive robust controllers for linear dynamic systems. Instead of converting it to a first-order state-space form of modern control theory, we take advantage of the second-order form of the dynamic equations to formulate these virtual passive controllers, and to prove the overall closed-loop system stability. The reason for doing is as follows. In first-order form, stability is usually proven through an eigenvalue analysis, and trying to show the guaranteed stability property of this type of controllers can be difficult. However, if the controller itself is a virtual second-order dynamic system, then the overall closed-loop system still remains in second-order form. Thus overall stability can be shown by simply proving certain matrices to be symmetric and positive definite (or positive semi-definite). This turns out to be a much more intuitively appealing and effective approach. Position, velocity, and acceleration feedback are considered in this formulation. For a very general formulation of this design approach, see Juang and Phan (1992).

Virtual Passive Control of Nonlinear Mechanical Systems

A general control design methodology has been outlined for large motion control and vibration suppression in multiple flexible-body dynamic systems. The method guarantees stability of the closed-loop control system. The approach is model-independent in the sense that knowledge of the system dynamics (linear or nonlinear) is not required in the design process. Hence, it is robust with respect to parameter variations. Required, however, is collocation of sensors and actuators. The design does not necessarily require velocity measurements for feedback stabilization. It can use position, acceleration, (or velocity) measurements, or any combination, and still guarantees stability of the closed loop system. One special case of the methodology demonstrates how one can obtain the desirable properties of velocity feedback using acceleration feedback, which is often easier to instrument in practice. The design has intuitive appeal in terms of its physical interpretation that aids the control design process. Global stability is proven using through the use of Liapunov functions. For more information see Juang, Wu, Phan, and Longman (1993).

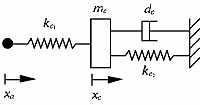
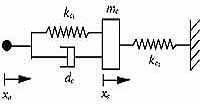
Illustration: One key feature of this formulation is that the controller gains have physical interpretation. Therefore one can visualize how the controller is removing energy from the system and tune the controller gains accordingly. The developed theory allows for a wide variety of designs, two of which are shown here for illustration. The design on the left corresponds to a virtual passive controller that requires only displacement feedback to stabilize the system. The design on the right corresponds to a combination of displacement and acceleration feedback. In both cases, the inclusion of the springs connected to the ground is necessary for position control, but not vital for vibration suppression. This special feature allows one to design vibration suppression controllers with accelerometer feedback alone. The corresponding diagram for this case is the same as the one given in the right figure with the spring connected to the ground removed. One can also "visualize" how each of these two designs can mimic the ideal case of velocity feedback for vibration suppression.