State-Space Theory of Learning Control
Learning control originated from robotics. Consequently, much of the early emphasis was on non-linear continuous-time dynamical systems, and robot dynamics in particular. One was more concerned with inventing various learning control laws, and then tried to show that such learning laws guarantee stability of the learning process. Less emphasis was placed on developing a comprehensive theory of learning control and its relationship to existing elements of system theory. As a result, there were rigorous proofs on the stability of a particular learning control law on robot dynamical equations, but little understanding was available on how a particular learning control law would work on on a simple linear model, or how best to design a learning controller when an approximate model of the system is available. One major aim of our research effort has been to establish a comprehensive theory of learning control, starting with linear time-invariant models, then moving systematically to linear time-varying models, and to non-linear models. To link it to much of modern control theory, first-order state-space model is used in the formulation. Because learning control requires storage of prior input and output time histories, discrete-time formulation is preferred over continuous-time one. This effort began as early as 1988, and to date, it has resulted in a sizable and comprehensive formulation of learning control, described in several dozens of publications, including many successful experimental results. These results together form a rigorous learning control component to modern control system theory. A summary of some of these results can be found in Phan and Frueh (1998).
It is also noted here why for both theoretical and practical reasons, the linear perspective (both time-invariant and time-varying) of the learning control problem is important. First, it provides a baseline knowledge against which non-linear learning control theory can be compared. Second, the linear perspective provides useful insights into the learning control problem which may otherwise be overlooked. Third and more importantly, the usefulness of this assumption has been confirmed repeatedly in practice on both linear and non-linear problems. There are various reasons for this:
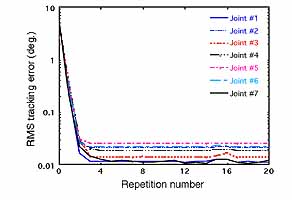
Illustration: A series of experiments was performed on a redundant 7 degree-of-freedom Robotics Research Corp. K-series 807iHP manipulator (left figure). The robot maximum workspace radius without tool is 0.89 m and maximum payload is 20 lbs. The existing analog controllers for each joint make extensive use of feedback compensators: position and velocity loops, a current loop on the amplifiers for the brushless DC motors, and torque loop driven by strain-gage feedback from the output side of the harmonic drive. The desired trajectories are specified in joint space since there is no sensor available on the robot tip. The same trajectory is specified for all joints. The trajectory contains cycloidal paths for a 90-degree turn followed by a return to the starting position. When all joints execute this trajectory, the robot produces a large movement from a contracted to an almost fully extended configuration and returns. The maximum speed along the trajectory is chosen to correspond to the maximum speed of the two joints closest to the base (55 deg/sec). This assures a high degree of dynamic coupling and maximization of non-linear effects to show the effectiveness of the learning control. The RMS tracking error due to the existing feedback controller in executing this rather extreme trajectory is between 5 and 6 degrees. When learning control is applied, this error for all 7 joints of the robot is brought down nearly a factor of 1000 after 4 iterations (right figure). The slight upward moment in the error at around repetition 15 is due to an unexpected power surge. The final error is at the repeatability level of the hardware (the limiting accuracy of learning control). Additional information can be found in Elci et al. (1994).


Learning Control with Basis Functions and Wavelets
Basis functions are important in learning control for several reasons. First, they can be used to represent input and output histories in a compact manner. In learning control, one deals with high-dimensional static input-output maps that relate a sampled input time history (say, 1000 points) to an sampled output time history (say, another 1000 points). For an arbitrary linear time-varying model, the number of parameters that are present in such a model is huge (say 1,000,000 parameters in this case). To identify such a map, the number of experiments that must be carried out can be prohibitedly large. When basis functions are used to represent input and output time histories, however, the dimension of the static input-output model becomes manageable, and the number of experiments that need to be carried out for learning control purpose is much less. This usage of basis functions is critical in learning control because without it, it may not practical to bring identification into learning control. Second, with basis functions, we know what portion of the system is being identified as more and more repetitions are made. This knowledge can be used to guide the learning controller by restraining it not to venture outside the domain for which it has little or no knowledge about, thus helping to make the learning process well-behaved. Third, the basis functions also allow the learning control input to be built up one basis function at a time. In this manner, the system can quickly learn to perform the gross motion first, and with additional refinement to follow as more and more basis functions are added. Additional information can be found in Phan and Frueh (1996), Frueh and Phan (1997), Phan and Rabitz (1997, 1999). Finally, with suitable basis functions, the repetitive control problem can be viewed as a learning control problem under rather mild assumptions, Wen, Phan, and Longman (1998). Conventional wisdom argues it is the other way around, i.e., learning control is a special case of repetitive control.
Advantages of Using Wavelets: When wavelets are used as basis functions, the number of identification experiments that one normally has to carry out is substantially reduced even further. Taking advantage of the translation property of compactly supported wavelets, and the time-invariant nature of the dynamics, pseudo-experiments can be inferred by simply time-shifting results of previous experiments. For example, to cover the 128-dimensional space of an 128-point input trajectory, only 41 experiments need to be carried out for identification purpose. The remaining 87 experiments are inferred by time-shifting. For longer trajectories, the saving is even more dramatic (e.g., only 9 or so additional experiments are need to cover a 256-dimensional input vector space, depending on the type of wavelets used). Additional information can be found in Frueh and Phan (1998).
Observation Spillover and Control Spillover in Learning Control
The literature on control of large flexible spacecraft defines the terms control spillover and observation spillover. In that context, one considers a system model containing a chosen number of vibration modes, and designs a controller and an observer that reconstructs the state and determines the control action. Control spillover refers to the control action exciting vibration modes that are not included in the model. Observation spillover refers to the control action being affected by part of the state not included in the model. When both control and observation spillovers are present, they can destabilize a system which appears to be stable based on the chosen model. However, if either one of these spillovers is zero, then stability of the control on the reduced-order model implies stability of the control on the full-order system. When using basis functions in learning control we can have an analogous situation. The control action we choose can excite parts of the output that are not in the space spanned by the chosen output basis functions (control spillover), and our measurements can contain parts of the output that are not in this space, and hence the control action is corrupted (observation spillover). We examine this situation and determine ways in which one or both types of spillovers can be eliminated. Additional information can be found in Wen, Phan, and Longman (1998).
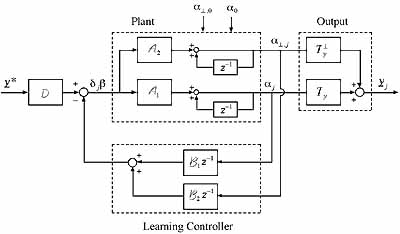
Illustration: The following is a graphical description of the structure of learning control using basis functions. The inverse z operator represents a backward shift of one repetition. The inner loop (A1 and B1) governs stability of the reduced-order model, whereas the outer loop describes how observation spillover (B2) and control spillover (A2) influence the overall system stability. If one designs a learning controller looking only in the basis function space, and ensuring stability for the inner loop (A1 and B1), one must examine the possibility for spillovers to destabilize the system when the control law is applied to the real world. This figure also shows that if either observation or control spillover is eliminated, then the outer loop is broken, thus stability of the inner loop guarantees stability of the overall system. In learning control, there are interesting and practical ways by which either or both kinds of spillovers can be eliminated.
Linear Quadratic Optimal Learning Control (LQL)
This is the learning control counterpart of the classic linear quadratic optimal control problem. The following is a formal statement of the problem. Consider a system of the general form
where A(k), B(k), C(k) are unknown. The initial state x(0), the process and output disturbances w(k) are also unknown, but assumed to be the same from one trial to the next. Given a desired trajectory specified over a finite time interval, k = 1, 2,..., p, the objective is to find the optimal control input u(k), k = 0, 1,..., p-1, by iterative learning so that the following cost function is minimized,
where e(k) is the tracking error (difference between desired and optimal output histories), R(k) and Q(k) are symmetric, positive definite, and positive semi-definite weighting matrices, respectively. It is assumed that only input and output data from iterative trials are available, and the state x(k) cannot be directly measured.
This is an important problem in its own right because with learning control, we have the opportunity to achieve optimality on the true system rather on its assumed model. When an optimal control input is synthesized one basis function at a time (for well-behaved learning), it is desirable that the optimal solution associated with the addition of a new input basis function will not alter the previously optimized coefficients of the existing basis functions. These so-called conjugate basis functions are dependent on the unknown system parameters and the known weighting factors in the cost function to be minimized. Yet it can be shown that these optimal basis functions that synthesize the optimal learning control input can be extracted using data from identification trials. A solution to this LQL problem is presented in Frueh and Phan (1998) including learning control results on an extremely lightly damped flexible test article called SPINE. This series of experiments is used to illustrate how this learning control technique can overcome unknown flexible dynamics. Being able to handle unknown flexible dynamics is very important in ultra-high precision tracking control problems. Conventional learning control and feedback control designs would have difficulties in handling this kind of problem.
Bridging Learning Control and Repetitive Control
Learning control aims at improving the tracking accuracy of a repetitive operation where the system is designed to return to the same initial condition before beginning the next repetition. Repetitive control, in contrast, deals with system executing a periodic command continuously without initial condition resetting. It appears that this distinction causes considerable difference between how learning control and repetitive control are treated in the literature. However, it has been observed in actual experiments that the distinction is not as pronounced as it seems mathematically. In this paper, we show how the repetitive control problem can be turned into a learning control problem through the use of basis functions. Repetitive disturbances may be present and unknown. We also examine the issue of observation and control spill over and show that by working in the basis function space, observation spill over is automatically eliminated. When matched basis functions are used, control spill over is also eliminated. The matched basis functions also eliminate the need to know a model of the system before hand. Instead, they are obtained experimentally. With wavelets, the process of extracting the matched basis functions experimentally becomes extremely efficient. Numerical examples are used to illustrate the key findings. Additional information can be found in Wen, Phan, and Longman (1998).
Learning Control of Quantum-Mechanical Systems
The prospect of controlling quantum phenomena are becoming a topic of ever broader interest in the chemistry and physics community. The essential element of control is the manipulation of quantum interferences, regardless of the application. Much of the theoretical efforts have addressed the development of conceptual and numerical machinery for designing optimal control fields. In practice, however, there is a serious lack of detailed quantitative information about the physical system being controlled, and it is virtually impossible to precompute a control field with sufficient accuracy that can steer a quantum process to a desired goal. A generic route to treating these problems is through various forms of feedback control. Unfortunately, most quantum processes occur on ultrafast time scales (pico-seconds), making it exceedingly difficult, if not impossible, to consider real-time feedback control. The appropriate type of technology for this application is iterative learning control which can be performed off-line at a more "leisurely" time scale. This prospect is especially attractive, given the availability of emerging optical pulse shaping tools, which can be adjusted at a high rate, so that many controlled pump-probe experiments (or trials) can be performed in the tradition of iterative learning in a short amount of time. Thus learning control is potentially an ideal tool that allows chemists and physicists to manipulate quantum processes at a high level of precision that is normally impossible to achieve. By repeated trials, the exact control field can be learned that compensates for the lack of knowledge of the quantum process under consideration, and the variable experimental parameters such as stray fields, collisions, and optical distortions. For more information see Quantum Control and Phan and Rabitz (1997, 1999).
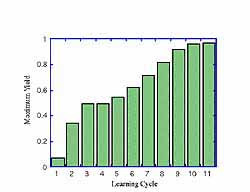
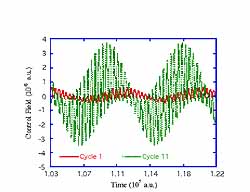
Illustration: A quantum mechanical system consisting of a ground level (level 1), a close lying excited level (level 2), and two energetically degenerate upper levels (levels 3 and 4) is used in this quantum control simulation. The objective of the problem is to drive the system from level 1 to level 4 in a prescribed amount of time. The measured output is the population of level 4. The system is driven by three constant amplitude laser pulses over the specified time interval, whose frequencies match those of the three transitions. Learning is carried out "from scratch" without any prior knowledge of the process dynamics. A sequence of intermediate desired trajectories (not shown explicitly in the figure) is successfully met by iterative trials designed from their respective input-output maps. During the entire process, input-output data used to identify the intermediate models for the next set of runs are obtained by perturbing the last learned values of the control coefficients from the previous set of runs. The left figure shows the transition eventually taking place with nearly perfect yield by iterative learning. The right figure shows a portion of the initial laser pulse shape versus that eventually obtained after learning.